CONJUNTO Y DIAGRAMA DE VENN

CONJUNTO.
1:En matemáticas, un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc. Se dice que un elemento (o miembro) pertenece al conjunto si está definido como incluido de algún modo dentro de él.
2:Un conjunto es la agrupación, clase, o colección de objetos o en su defecto de elementos que pertenecen y responden a la misma categoría o grupo de cosas, por eso se los puede agrupar en el mismo conjunto. Esta relación de pertenencia que se establece entre los objetos o elementos es absoluta y posiblemente discernible y observable por cualquier persona. Entre los objetos o elementos susceptibles de integrar o conformar un conjunto se cuentan por supuesto cosas físicas, como pueden ser las mesas, sillas y libros, pero también por entes abstractos como números o letras.
3:e denomina conjunto a la agrupación de entes o elementos, que poseen una o varias características en común. Es un concepto intuitivo empleado en matemática, que elaboró la teoría de conjuntos. Para saber si un conjunto está bien definido habrá que atender a la siguiente regla: cuando la pertenencia de un elemento a un conjunto es clara, el conjunto estará bien definido. Por ejemplo, nadie dudaría de incluir al Domingo entre los días de la semana, pero el conjunto de personas rubias no está bien definido, pues hay dudas si determinadas personas pertenecen o no al conjunto, pues la calidad de rubio no es precisa.
DIAGRAMA DE VENN.

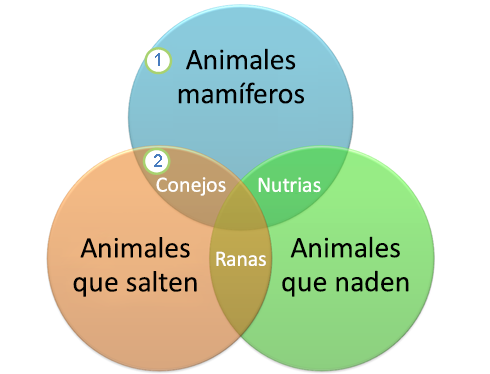
Los diagramas de Venn son esquemas usados en la teoría de conjuntos, tema de interés en matemáticas, lógica de clases y razonamiento diagramático. Estos diagramas muestran colecciones (conjuntos) de cosas (elementos) por medio de líneas cerradas. La línea cerrada exterior abarca a todos los elementos bajo consideración, el conjunto universal U.

Los diagramas de Venn fueron ideados hacia 1880 por John Venn.

ejemplo:

OPERACIONES BASICAS DE CONJUNTO:

• Pertenencia. La relación relativa a conjuntos más básica es la relación de pertenencia. Dado un elemento x, éste puede o no pertenecer a un conjunto dado A. Esto se indica como:

${\displaystyle x\in A\quad \longrightarrow }$ x pertenece a A.

${\displaystyle x\notin A\quad \longrightarrow }$ x no pertenece a A.

• Igualdad. Dos conjuntos son iguales si y sólo si tienen los mismos elementos. Este principio, denominado principio de extensionalidad establece el hecho de que un conjunto queda definido únicamente por sus elementos

${\displaystyle A=B\quad \longrightarrow }$ A es igual a B.

${\displaystyle A\neq B\quad \longrightarrow }$ A no es igual a B.

• Inclusión. Dado un conjunto A, cualquier subcolección B de sus elementos es un subconjunto de A, y se indica como:

${\displaystyle A\subseteq B\quad \longrightarrow }$A es un subconjunto de B.

${\displaystyle A\nsubseteq B\quad \longrightarrow }$ A no es subconjunto de B.

Leyes de identidad[editar]

• A ∪ ${\displaystyle \emptyset }$ = A, la unión de un conjunto cualquiera con el conjunto vacío es el mismo conjunto.
• A ∩ U = A, la intersección de un conjunto cualquiera con el conjunto universal es el mismo conjunto.

Leyes de dominación[editar]

• A ∪ U = U, la unión de un conjunto cualquiera con el conjunto universal, es el conjunto universal.
• A ∩ ${\displaystyle \emptyset }$ = ${\displaystyle \emptyset }$, la intersección de un conjunto cualquiera con el conjunto vacío, es el conjunto vacío.

Leyes idempotentes[editar]

• A ∪ A = A, la unión de un conjunto cualquiera consigo mismo, es el mismo conjunto.
• A ∩ A = A, la intersección de un conjunto cualquiera consigo mismo, es el mismo conjunto.

Ley de complementación[editar]

• A, la negación de la negación de un conjunto cualquiera, es el mismo conjunto.

Leyes conmutativas[editar]

• A ∪ B = B ∪ A
• A ∩ B = B ∩ A

Leyes asociativas[editar]

• A ∪ (B∪C) = (A∪B) ∪ C
• A ∩ (B∩C) = (A∩B) ∩ C

Leyes distributivas[editar]

• A ∩ (B∪C) = (A∩B) ∪ (A∩C)
• A ∪ (B∩C) = (A∪B) ∩ (A∪C)

Leyes de De Morgan[editar]

Representación gráfica de las leyes de De Morgan

• A ∪ B = A ∩ B
• A ∩ B = A ∪ B

La forma generalizada es:

${\displaystyle {\overline {\bigcap _{i\in I}A_{i}}}\equiv \bigcup _{i\in I}{\overline {A_{i}}}}$

${\displaystyle {\overline {\bigcup _{i\in I}A_{i}}}\equiv \bigcap _{i\in I}{\overline {A_{i}}}}$

donde I es un conjunto indexado, posiblemente incontable.

Leyes de absorción[editar]

• A ∪ (A∩B) = A
• A ∩ (A∪B) = A

Leyes de complemento[editar]

• A ∪ A = U, la unión de un conjunto cualquiera con su complementario, es el conjunto universal.
• A ∩ A = ${\displaystyle \emptyset }$, la intersección de un conjunto cualquiera con su complementario, es el conjunto vacío.

OPERACIÓN CON DIAGRAMA DE VENN

Uniones e intersecciones generalizadas

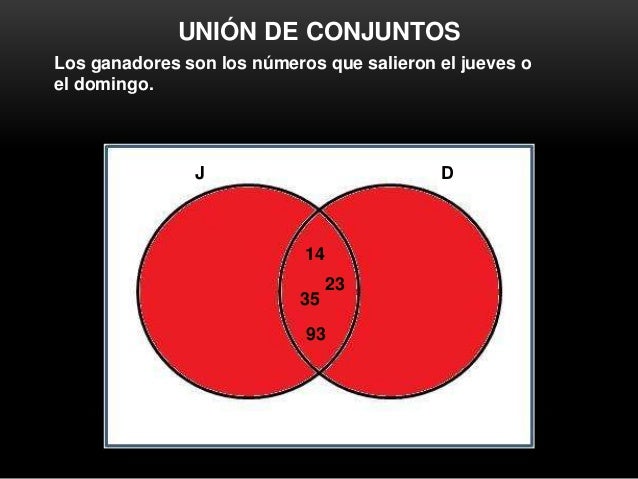
Las operaciones de unión y de intersección tienen la propiedad asociativa, por lo tanto si tenemos tres conjuntos A, B y C...

La unión de esos tres conjuntos es otro conjunto D el cual contiene todos aquellos elementos que están al menos en uno de los conjuntos A, B o C. (A∪B∪C)

Un elemento x pertenece a la unión de los conjuntos A, B y C si, y sólo si, x pertenece al conjunto A o x pertenece al conjunto B o x pertenece al conjunto C, por lo tanto: 

La intersección de los conjuntos A, B y C queda como resultado otro conjunto D el cual tiene los elementos que están estrictamente en A, en B y en C. (A∩B∩C)

Un elemento x pertenece a la intersección de los conjuntos A, B y C si, y sólo si, x pertenece al conjunto A, x pertenece al conjunto B y x pertenece al conjunto C, por lo tanto: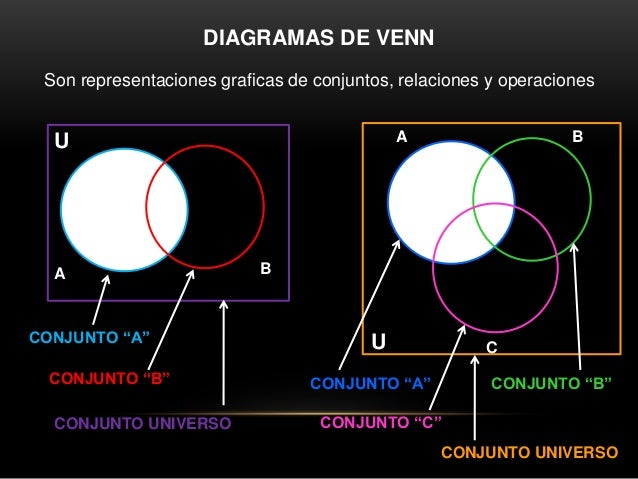 

EJERCICIOS:

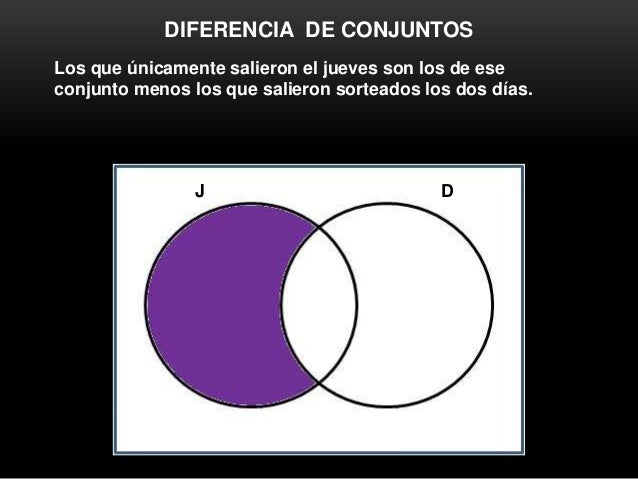
TABLAS DE VERDAD

Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.

Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.

TABLA DE KAMAUGH:

Un mapa de Karnaugh (también conocido como tabla de Karnaugh o diagrama de Veitch, abreviado como Mapa-K o Mapa-KV) es un diagrama utilizado para la simplificación de funciones algebraicas Booleanas. El mapa de Karnaugh fue inventado en 1950 por Maurice Karnaugh, un físico y matemático de los laboratorios Bell.

Los mapas de Karnaugh reducen la necesidad de hacer cálculos extensos para la simplificación de expresiones booleanas, aprovechando la capacidad del cerebro humano para el reconocimiento de patrones y otras formas de expresión analítica, permitiendo así identificar y eliminar condiciones muy inmensas.

DIFERENCIA ENTRE TABLA DE VERDAD Y TABLA DE KAMAUGH:

n cambio en Karnaugh vos tenes esa misma información pero ordenada de forma tal que podes hallar la función lógica simplificada que representa al circuito. Karnaugh sirve para eso...simplificar las expresiones.